Uncertainty Quantification

Only in very rare cases are the inputs and parameters of a model known exactly. Usually, inputs and parameter values come from measurements done in the field or in the lab, and those measurements are never exact. So every model is subject to uncertainty. Uncertainty Quantification (UQ) provides techniques for analysing th uncertainty in models, parameters and results. This section shows an example of a black-box quasi-Monte Carlo uncertainty quantification of the reaction-diffusion model we created before, implemented using MUSCLE3.

Simulation design

Let’s start with an overview in the form of a gMMSL diagram of the set-up.

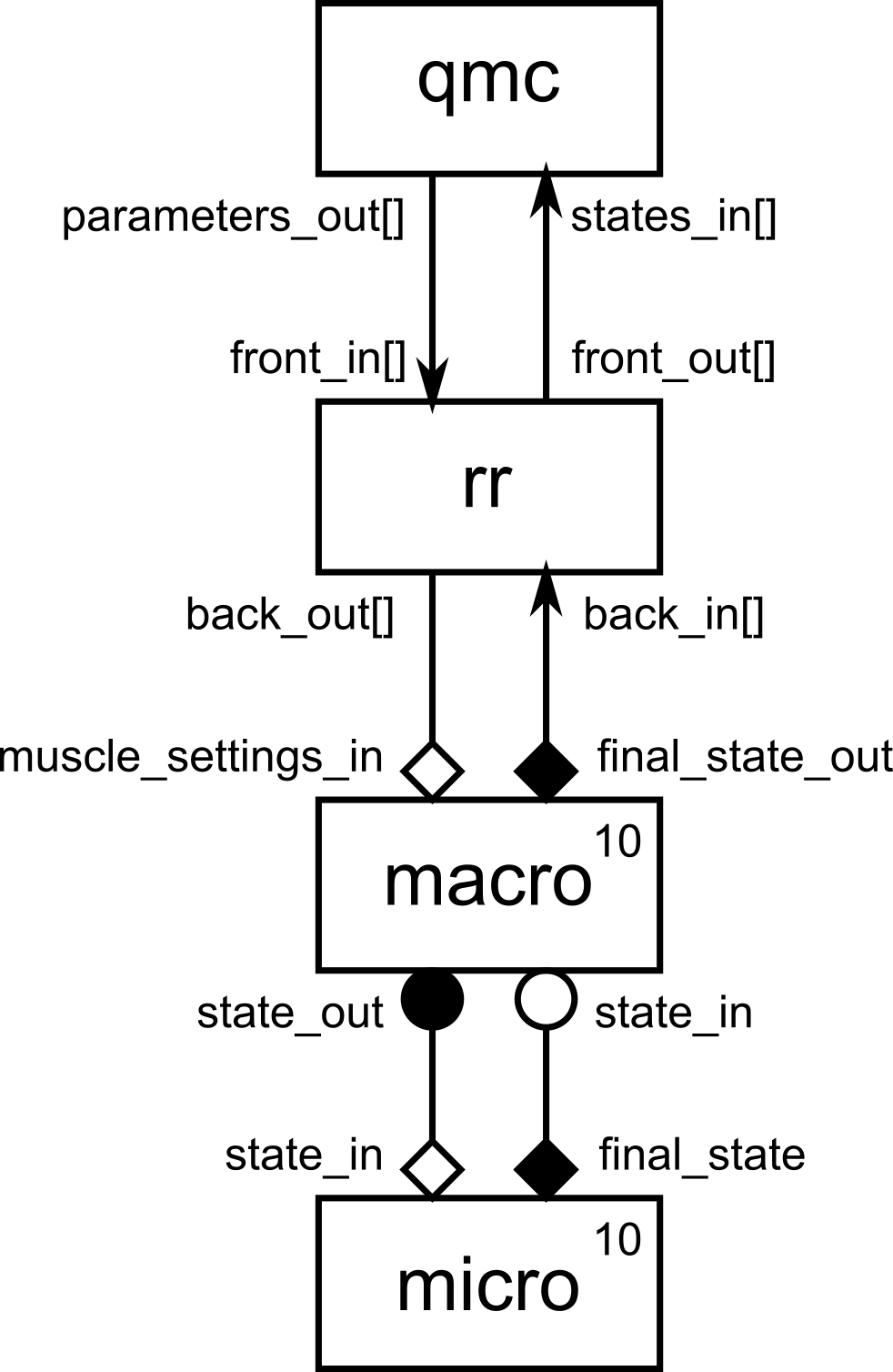
gMMSL diagram of the qMC reaction-diffusion simulation set-up.

At the bottom, we have the macro-micro model we saw earlier. The reaction model is exactly identical to the previous example. For the diffusion model we have removed the visualisation and instead send the final state on an output port final_state_out associated with the O_F operator. (It would probably have been good to do that to begin with, using a separate visualisation or save-to-disk component attached via a conduit.) The only other change here is that there are now ten copies each of the macro and micro components. There will also be ten instances of the conduits between macro and micro, which MUSCLE3 will create automatically. The instances are wired up one-on-one, so that macro[i] connects to micro[i].

There are two new components: the qmc element, which implements the quasi-Monte Carlo UQ algorithm, and the rr element, which distributes the ensemble evenly over a given number of model instances.

The quasi-Monte Carlo component is not a submodel, since it does not actually model any real-world system. In MUSCLE/MMSL terminology it is a type of component called a Proxy. We’ll not get into the theoretical differences here, but just have a practical look at how it works.

We will assume that the model parameters k and d of the reaction and diffusion models are uncertain, and have a uniform distribution ranging from -10% to +10% of their original values. The qmc component will generate a quasi-random sample of the resulting box in the input parameter space, resulting in a set of parameter values {(k, d)}. It writes these parameters to its parameters_out port.

The name of this port in the diagram ends in a pair of square brackets, which designates the port a vector port. A vector port is a port that is used to talk to multiple instances of a connected components. It has a number of slots on which messages can be sent (or received, if it is a receiving port). The number of slots is known as the length of a vector port. Since we are going to run an ensemble, and we want to be able to run the ensemble members in parallel, having a set of concurrent instances is just what we need. Of course, we will then receive results from this same set as well, so we’ll receive on a vector port too, in this case states_in.

The qmc.parameters_out port will have a length equal to the size of the sample set it produces. This number may well be larger than the number of instances of the model we can accomodate given the size of our compute facilities. The rr component solves this issue by taking the messages it receives on its front_in vector port, and distributing them evenly amongst the slots of its back_out vector port in a round-robin fashion (hence the name). The length of front_in matches that of qmc.parameters_out, while the length of back_out matches the number of instances of macro. The returning final states will be mapped back accordingly.

Next, rr needs to be connected to the model. This presents a problem: rr sends out sets of parameters, but macro has no F_INIT port to receive them. It gets its parameter values, via MUSCLE3, from the central configuration. So we need a trick, and MUSCLE3 provides one in the form of the muscle_settings_in port. This is a special F_INIT port that each MUSCLE3 component automatically has. It can be connected to a port on a component that sends Settings objects. MUSCLE3 will automatically receive these messages, and overlay the received settings on top of the base settings from the central configuration. When the receiving submodel then asks MUSCLE3 for a setting, MUSCLE3 will look at the overlay settings first. If the setting is not found there, then MUSCLE3 will fall back to the central base configuration.

So, now our diffusion model will ask for the value of d as it did before, but this time, it will actually come from the values sent by qmc, and it will be different for each instance of the diffusion model. In a way, each instance lives in its own universe, with its own universal constants. It is unaware of this however; to the diffusion model instance everything looks just the same as in the previous example when it was the only one around.

The one remaining piece of the puzzle is that the universe will be automatically extended: overlay parameters that were sent from the rr component to a macro-model instance will automatically be passed on to the corresponding micro-model instance. In this way, each k parameter value arrives at the reaction model that needs it.

Implementation

The full Python program implementing this looks like this:

docs/source/examples/python/reaction_diffusion_qmc.py

import logging
import os

import numpy as np
import sobol_seq

from libmuscle import Grid, Instance, Message, DONT_APPLY_OVERLAY
from libmuscle.runner import run_simulation
from ymmsl import (
        Component, Conduit, Configuration, Model, Operator, Ports, Settings)


def reaction() -> None:
    """A simple exponential reaction model on a 1D grid.
    """
    instance = Instance({
            Operator.F_INIT: ['initial_state'],     # 1D Grid
            Operator.O_F: ['final_state']})         # 1D Grid

    while instance.reuse_instance():
        # F_INIT
        t_max = instance.get_setting('t_max', 'float')
        dt = instance.get_setting('dt', 'float')
        k = instance.get_setting('k', 'float')

        msg = instance.receive('initial_state')
        U = msg.data.array.copy()

        t_cur = msg.timestamp
        while t_cur + dt < msg.timestamp + t_max:
            # O_I

            # S
            U += k * U * dt
            t_cur += dt

        # O_F
        instance.send('final_state', Message(t_cur, data=Grid(U, ['x'])))


def laplacian(Z: np.array, dx: float) -> np.array:
    """Calculates the Laplacian of vector Z.

    Args:
        Z: A vector representing a series of samples along a line.
        dx: The spacing between the samples.

    Returns:
        The second spatial derivative of Z.
    """
    Zleft = Z[:-2]
    Zright = Z[2:]
    Zcenter = Z[1:-1]
    return (Zleft + Zright - 2. * Zcenter) / dx**2


def diffusion() -> None:
    """A simple diffusion model on a 1d grid.

    The state of this model is a 1D grid of concentrations. It sends
    out the state on each timestep on `state_out`, and can receive an
    updated state on `state_in` at each state update.
    """
    instance = Instance({
            Operator.O_I: ['state_out'],
            Operator.S: ['state_in'],
            Operator.O_F: ['final_state_out']})

    while instance.reuse_instance():
        # F_INIT
        t_max = instance.get_setting('t_max', 'float')
        dt = instance.get_setting('dt', 'float')
        x_max = instance.get_setting('x_max', 'float')
        dx = instance.get_setting('dx', 'float')
        d = instance.get_setting('d', 'float')

        U = np.zeros(int(round(x_max / dx)))
        U[25] = 2.0
        U[50] = 2.0
        U[75] = 2.0
        Us = U

        t_cur = 0.0
        while t_cur + dt <= t_max:
            # O_I
            t_next = t_cur + dt
            if t_next + dt > t_max:
                t_next = None
            cur_state_msg = Message(t_cur, t_next, Grid(U, ['x']))
            instance.send('state_out', cur_state_msg)

            # S
            msg = instance.receive('state_in', default=cur_state_msg)
            if msg.timestamp > t_cur + dt:
                logger.warning('Received a message from the future!')
            np.copyto(U, msg.data.array)

            dU = np.zeros_like(U)
            dU[1:-1] = d * laplacian(U, dx) * dt
            dU[0] = dU[1]
            dU[-1] = dU[-2]

            U += dU
            Us = np.vstack((Us, U))
            t_cur += dt

        # O_F
        instance.send('final_state_out', Message(t_cur, data=Grid(U, ['x'])))


def load_balancer() -> None:
    """A proxy which divides many calls over few instances.

    Put this component between a driver and a set of models, or between
    a macro model and a set of micro models. It will let the driver or
    macro-model submit as many calls as it wants, and divide them over
    the available (micro)model instances in a round-robin fashion.

    Assumes a fixed number of micro-model instances.

    Ports:
        front_in: Input for calls, connect to driver/macro-model O_I.
        back_out: Output to workers, connect to F_INIT of instances that
                do the work.
        back_in: Input for results, connect to O_F of instances that do
                the work.
        front_out: Output back to driver/macro-model S.
    """
    instance = Instance({
            Operator.F_INIT: ['front_in[]'],
            Operator.O_I: ['back_out[]'],
            Operator.S: ['back_in[]'],
            Operator.O_F: ['front_out[]']},
            DONT_APPLY_OVERLAY)

    while instance.reuse_instance():
        # F_INIT
        started = 0     # number started and index of next to start
        done = 0        # number done and index of next to return

        num_calls = instance.get_port_length('front_in')
        num_workers = instance.get_port_length('back_out')

        instance.set_port_length('front_out', num_calls)
        while done < num_calls:
            while started - done < num_workers and started < num_calls:
                msg = instance.receive_with_settings('front_in', started)
                instance.send('back_out', msg, started % num_workers)
                started += 1
            msg = instance.receive_with_settings('back_in', done % num_workers)
            instance.send('front_out', msg, done)
            done += 1


def qmc_driver() -> None:
    """A driver for quasi-Monte Carlo Uncertainty Quantification.

    This component attaches to a collection of model instances, and
    feeds in different parameter values generated using a Sobol
    sequence.
    """
    instance = Instance({
            Operator.O_I: ['parameters_out[]'],
            Operator.S: ['states_in[]']})

    while instance.reuse_instance():
        # F_INIT
        # get and check parameter distributions
        n_samples = instance.get_setting('n_samples', 'int')
        d_min = instance.get_setting('d_min', 'float')
        d_max = instance.get_setting('d_max', 'float')
        k_min = instance.get_setting('k_min', 'float')
        k_max = instance.get_setting('k_max', 'float')

        if d_max < d_min:
            instance.error_shutdown('Invalid settings: d_max < d_min')
            exit(1)
        if k_max < k_min:
            instance.error_shutdown('Invalid settings: k_max < k_min')
            exit(1)

        # generate UQ parameter values
        sobol_sqn = sobol_seq.i4_sobol_generate(2, n_samples)
        ds = d_min + sobol_sqn[:, 0] * (d_max - d_min)
        ks = k_min + sobol_sqn[:, 1] * (k_max - k_min)

        # configure output port
        if not instance.is_resizable('parameters_out'):
            instance.error_shutdown(
                    'This component needs a resizable parameters_out port, but'
                    ' it is connected to something that cannot be resized.'
                    ' Maybe try adding a load balancer.')
            exit(1)

        instance.set_port_length('parameters_out', n_samples)

        # run ensemble
        Us = None
        # O_I
        for sample in range(n_samples):
            uq_parameters = Settings({
                'd': ds[sample],
                'k': ks[sample]})
            msg = Message(0.0, data=uq_parameters)
            instance.send('parameters_out', msg, sample)

        # S
        for sample in range(n_samples):
            msg = instance.receive_with_settings('states_in', sample)
            U = msg.data.array
            # accumulate
            if Us is None:
                Us = U
            else:
                Us = np.vstack((Us, U))

        mean = np.mean(Us, axis=0)

        # O_F
        if 'DONTPLOT' not in os.environ:
            from matplotlib import pyplot as plt

            t_max = instance.get_setting('t_max', 'float')
            dt = instance.get_setting('dt', 'float')
            x_max = instance.get_setting('x_max', 'float')
            dx = instance.get_setting('dx', 'float')

            plt.figure()
            plt.imshow(
                    np.log(Us + 1e-20),
                    origin='upper',
                    extent=[
                        -0.5*dx, x_max - 0.5*dx,
                        n_samples-0.5, -0.5],
                    interpolation='none',
                    aspect='auto'
                    )
            cbar = plt.colorbar()
            cbar.set_label('log(Concentration)', rotation=270, labelpad=20)
            plt.xlabel('x')
            plt.ylabel('Sample')
            plt.title('Final states')
            plt.show()


if __name__ == '__main__':
    logging.basicConfig()
    logging.getLogger().setLevel(logging.INFO)

    components = [
            Component(
                'qmc', 'qmc_driver', None,
                Ports(o_i=['parameters_out'], s=['states_in'])),
            Component(
                'rr', 'load_balancer', None,
                Ports(
                    f_init=['front_in'], o_i=['back_out'],
                    s=['back_in'], o_f=['front_out'])),
            Component(
                'macro', 'diffusion', [10],
                Ports(
                    o_i=['state_out'], s=['state_in'], o_f=['final_state_out']
                    )),
            Component(
                'micro', 'reaction', [10],
                Ports(f_init=['initial_state'], o_f=['final_state']))]

    conduits = [
            Conduit('qmc.parameters_out', 'rr.front_in'),
            Conduit('rr.front_out', 'qmc.states_in'),
            Conduit('rr.back_out', 'macro.muscle_settings_in'),
            Conduit('macro.final_state_out', 'rr.back_in'),
            Conduit('macro.state_out', 'micro.initial_state'),
            Conduit('micro.final_state', 'macro.state_in')
            ]

    model = Model('reaction_diffusion_qmc', components, conduits)
    settings = Settings({
        'micro.t_max': 2.469136e-6,
        'micro.dt': 2.469136e-8,
        'macro.t_max': 1.234568e-4,
        'macro.dt': 2.469136e-6,
        'qmc.t_max': 1.234568e-4,
        'qmc.dt': 2.469136e-6,
        'x_max': 1.01,
        'dx': 0.01,
        'k_min': -4.455e4,
        'k_max': -3.645e4,
        'd_min': 0.03645,
        'd_max': 0.04455,
        'n_samples': 100
        })

    configuration = Configuration(model, settings)

    implementations = {
            'qmc_driver': qmc_driver,
            'load_balancer': load_balancer,
            'diffusion': diffusion,
            'reaction': reaction}
    run_simulation(configuration, implementations)

The reaction model’s implementation is completely unchanged, and the diffusion model has only been made a bit more modular by removing the visualisation and sending the final state on an additional O_F port, as mentioned above. The qmc and rr components are new however, and deserve a detailed explanation.

The quasi-Monte Carlo element

The purpose of the qMC component is to generate a set of quasi-random pairs of parameters (k, d), and pass these to the individual members of the ensemble of models we will run. It receives back the final state of the simulation of each ensemble member, and then calculates the ensemble mean final state.

instance = Instance({
        Operator.O_I: ['parameters_out[]'],
        Operator.S: ['states_in[]']})

The qMC component does not require any input messages to initialise, and it does not produce a final result as a message (it makes a plot instead). It just sends out a single set of parameter pairs, and receives back a single set of final states. In terms of communication with the outside world, it therefore works similarly to a submodel with only O_I and S ports and exactly one state update step, so that each of those operators is run once. So that is how we describe it to MUSCLE3. We will send parameter sets on vector port parameters_out, and receive final states on vector port states_in.

Next, we enter the reuse loop as before, except that we pass False as an argument, which will be explained shortly. We read and check settings in F_INIT as before, and calculate a set of parameter values using a quasi-random Sobol sequence.

# configure output port
if not instance.is_resizable('parameters_out'):
    instance.error_shutdown(
            'This component needs a resizable parameters_out port, but'
            ' it is connected to something that cannot be resized.'
            ' Maybe try adding a load balancer.')
    exit(1)

instance.set_port_length('parameters_out', n_samples)

Next, we need to configure our output vector port. Since we will have n_samples sets of parameters, we will resize the port to that length. We do need to check whether the port is resizable first, because that may or may not be the case depending on what is attached to it. In order to preserve modularity and reusability of individual components, MUSCLE3 tries to tell the components as little as possible about what is on the other side of a port, but you can ask it whether the port has a fixed size or not.

So that is what we do here, and we generate an error message if the port’s length is fixed. We use the function libmuscle.Instance.error_shutdown() for this. This function will log the error, and then tell the rest of the simulation that we are shutting down. Doing this instead of raising an exception reduces the chance that any part of the simulation will sit around waiting forever for a message we will never send, and the log will show the origin of the problem for easier debugging. In this case, the port will be resizable and it will work as intended.

for sample in range(n_samples):
    uq_parameters = Settings({
        'd': ds[sample],
        'k': ks[sample]})
    msg = Message(0.0, data=uq_parameters)
    instance.send('parameters_out', msg, sample)

Since we only run our O_I and S once, we do not have a state update loop that advances the simulation time. We do however need to loop through all of our samples, and send a message on parameters_out for each one.

First, we create a Settings object that contains the parameters we are going to send. This is the same Settings class we used before to define the model configuration. Here, we only have d and k in there, since those are the only ones we need to set per ensemble member; the rest is identical and defined in the central configuration.

Next, we create a libmuscle.Message object to send. Since our models will start at time 0, we’ll set that as the timestamp, and since we’re only running them once each, we omit the next timestamp. For the data, we send the Settings object. (MUSCLE3 contains special support for sending Settings objects, since being objects they’re not normally MessagePack-serialisable.)

We then send our message as normal, except that we pass an extra argument, the slot number. Vector ports connect to sets of instances, and the slot number selects the exact instance to send the message to. They’re zero-based, so if the length of the vector port is 10, then the valid slot range is [0..9]. We resized our port to the number of samples before, so each sample has a corresponding slot for us to send on.

for sample in range(n_samples):
    msg = instance.receive_with_settings('states_in', sample)

When the reaction-diffusion models are done, they will send their final states back to us, so we need to receive those now. This is effectively our S operator. For each sample, we receive the result on our states_in port, passing the sample number as the slot to receive on. We’re using a slightly different receive function here. Rather than libmuscle.Instance.receive(), we call libmuscle.Instance.receive_with_settings(). The difference has to do with the settings overlays.

Recall that each component instance has a settings overlay, which can be set through the muscle_settings_in port and is automatically propagated to corresponding instances of other components. This propagation is done by sending the overlay along with any messages that are sent.

Since the macro and micro instances are connected one-on-one, each pair lives in its own universe with its own settings, unaware of the other pairs and their settings. Once the reaction-diffusion simulation is done however, the macro instances all send their result to a single qmc instance (via rr, which is transparent in this respect). Thus, the universes meet, and the question arises what the settings overlay for qmc should look like.

As there is no general answer to this, MUSCLE3 cannot automatically propagate the overlay from the different macro instances to qmc, and it will give an error message if you try to have it do this by receiving as usual with libmuscle.Instance.receive(). The libmuscle.Instance.receive_with_settings() function solves this problem, and is in a way the counterpart of sending a message to muscle_settings_in. It will not try to merge the incoming settings overlay into the overlay for qmc, but simply return it as the settings attribute of the received message. It is then up to the receiver to decide what to do with it.

In this case, we ignore the settings, concatenate all the received states together, plot them, and calculate the mean final state. You will probably want to do a more complex analysis (for which the settings may be very useful!), or save the raw data to disk for later processing.

The round-robin load balancer

The round-robin load balancer has the job to sit between the qmc element and the macro model, and distribute the many parameter sets qmc produces over a limited number of macro model instances. It has a front side, which connects to qmc, and a back side, which connects to macro.

instance = Instance({
        Operator.F_INIT: ['front_in[]'],
        Operator.O_I: ['back_out[]'],
        Operator.S: ['back_in[]'],
        Operator.O_F: ['front_out[]']},
        DONT_APPLY_OVERLAY)

while instance.reuse_instance():
    # F_INIT
    started = 0     # number started and index of next to start
    done = 0        # number done and index of next to return

    num_calls = instance.get_port_length('front_in')
    num_workers = instance.get_port_length('back_out')

    instance.set_port_length('front_out', num_calls)
    while done < num_calls:
        while started - done < num_workers and started < num_calls:
            msg = instance.receive_with_settings('front_in', started)
            instance.send('back_out', msg, started % num_workers)
            started += 1
        msg = instance.receive_with_settings('back_in', done % num_workers)
        instance.send('front_out', msg, done)
        done += 1

In order to distribute the messages correctly, we first need to determine the number of messages we’ll receive from qmc, as well as how many macro instances we have. We can determine this from the lengths of the corresponding vector ports. Since front_out is connected to another vector port, it does not have an intrinsic size, and we need to set the size explicitly to match front_in.

Next, we process messages, reading them from front_in and forwarding them to back_out, always sending each macro instance one message at a time, and making sure that for each message we send on back_out, we receive one on back_in. (We could actually send multiple messages on the same slot before receiving a result, they’ll be queued up and processed in order.)

We use libmuscle.Instance.receive_with_settings() everywhere, in order to correctly pass on any settings overlays. Since we are using libmuscle.Instance.receive_with_settings() on an F_INIT port, we passed libmuscle.InstanceFlags.DONT_APPLY_OVERLAY as flag when creating the libmuscle.Instance. It is a technical requirement of MUSCLE3 to do this, and MUSCLE will give an error message if you call libmuscle.Instance.receive_with_settings() without having set the libmuscle.InstanceFlags.DONT_APPLY_OVERLAY flag when creating the libmuscle.Instance.reuse_instance. (There’s just no other way to implement this, or rather, all other options can lead to potentially difficult-to-debug situations, while this can be checked and a clear error message shown if it goes wrong. So we chose this as the preferable option.)

Discussion

There are a few interesting things to remark here. First, the original model code is essentially unchanged. All the changes needed to do Uncertainty Quantification have been at the level of the couplings between the models. MUSCLE encourages modularity and reuse of models, and this example shows the benefits of this approach.

Second, we can see the beginnings of a library of reusable components. The round-robin load balancer shown here is completely model-agnostic, and in a future version of MUSCLE3 will become a built-in standard component for general use. There are other such components that can be made, such as the duplication mapper that MUSCLE 2 already has. With a small extension to MUSCLE, the qmc component here can also be made generic and model-agnostic. While some helper components will likely remain model-specific (such as scale bridges and data converters), we expect that modeling complex systems and performing UQ on them can be made significantly simpler using this approach.

The load balancer component described here uses a round-robin algorithm to distribute work. This works well in this case, with all model runs taking approximately the same amount of compute time. In general however, a more flexible algorithm is desirable, which would require another small extension to MUSCLE3. We plan to add this in a future version.

Examples in C++ and Fortran

MUSCLE3 comes with C++ and Fortran versions of this Uncertainty Quantification use case. They can be run like the other models, but use rdmc_settings.ymmsl instead of rd_settings.ymmsl. The models themselves are in rdmc_cpp.ymmsl and rdmc_fortran.ymmsl. The source code for the components may be found in docs/source/examples/cpp and docs/source/examples/fortran.